放物線の頂点の座標を求めよう～平方完成が苦手なあなたへ～

寒くなりました！今日は風が強く，山あいを吹き抜ける風が木々を揺らして木の葉が舞っています🍂

庭のマユミ（真弓）の実が熟して赤みが増し，皮が割れて中から真っ赤な種が顔を

のぞかせています。ピンクと赤のコントラストが美しく，華やかです。去年よりもたくさん実をつけたマユミ，たくましく育っています☺️

この時期になるとヒヨドリなどがやってきては実をついばみます。鳥たちを見るのもまた

楽しみです。

🌿さて，今回は久しぶりの「放物線」です。

冬休みに「２次関数」の内容を復習をする人もいるでしょう。グラフをかくときには必要な式変形や軸の方程式・頂点の座標など……。「苦手なんだなぁ」と思っているあなたに贈ります🎁

この内容は，普通は授業でも説明しません。慣れないうちに色々言うと，混乱しますから。

何かのついでにコメントしたり，平方完成による式変形が苦手な生徒に教えたりする程度

です。少しでも誰かの参考になると嬉しいです✨

では，次の問題で見ていきましょう！

🌺問題：

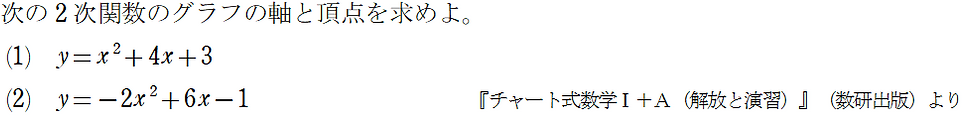
💚(1) の解答例：

💛まずは，普通の解き方から（グラフは参考）

💛では次に，さも式変形したように見えるけれど実際は当てはめただけの解答を

　ご紹介。

※ 「ウラ」は本当に裏の作業です。表（オモテ）に書くと，「説明不十分」とか「根拠不明」などと

　されて不可になりますので，要らないことは書かないことです。

　もし書くなら，この下の解説の内容をきちんと書くべし。

●なぜこのようにすれば解けるのか，下に解説を書きました。読むと頭が痛くなりそうな

　人は読み飛ばしてくださいね。

　　◎この解法のメリットは，はじめに定数項を除いて考えるので，グラフと x 軸との交点の１つは

　　　必ず原点になるということです。２つの交点の中点の座標を求めるのが簡単です。

何だか簡単に解けそう！と思った人は，(2) を解いてみてくださいね !(^^)!

💚(2) の解答例：（一般的な解答例を示しています。x２乗の係数が１以外の数だったり，分数が出てくるような

　　　　　　　　　　ものは，今回ご紹介した考え方が楽でいいかもしれませんね。）

🌿「数学Ⅰ」の内容の中で，苦手な人も多い「２次関数」。でも，高校数学では重要な内容

　なんです。この休みにまとまった時間をとって，じっくり向き合ってみてくださいね。

　「解けるかも」「ちょっと面白くなってきた」などと感じたら，きっと２次関数とは

　お友達になれますよ (^-^)

💕他の放物線の記事はこちら

　　　➣ 身近なところに潜む数学……放物線　前編後編

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（次回の記事は１月９日です）

早いもので，今年もあとわずかとなりました。今年はどんな一年だったでしょうか。

世の中は普通の生活に戻りましたが，集団風邪による学級閉鎖のニュースは絶えず，救急車のサイレンが昼夜問わず聞こえてきます。日本がこれからどうなっていくのだろうと思う

こともあり，一歩外に出れば別世界のようです。

環境が悪化する中でもこの一年を無事に過ごせたことに感謝いたします。

年末の掃除と共に，自分を振り返って楽しいこと・悲しいことなどを神に捧げて魂の

大掃除。自分の中の悪いものを受け入れていると，私たちを丸ごと受け入れてくださって

いる神様の深い愛を感じます。少しでもきれいになって新年を迎えたいと思います。

冬来たりなば春遠からじ，待ち望んだ春はもうそこまで来ています。

　　　　　　　　💗この一年，皆様には大変お世話になりました。

　　　　　　　　　拙い記事も読んでいただきまして，心より感謝申し上げます。

　　　　　　　　皆様お元気で良いお年をお迎えください。